Methods

Binary Trees

Trees are a special type of data structure because they are made up of a collection of nodes connected by edges. There isn’t a one stop initializer to create a new, generic tree like the other data structures we’ve looked at. To make things easier, we will look specifically at Binary Trees, which are a specific type of tree with strict rules about where each node should go.

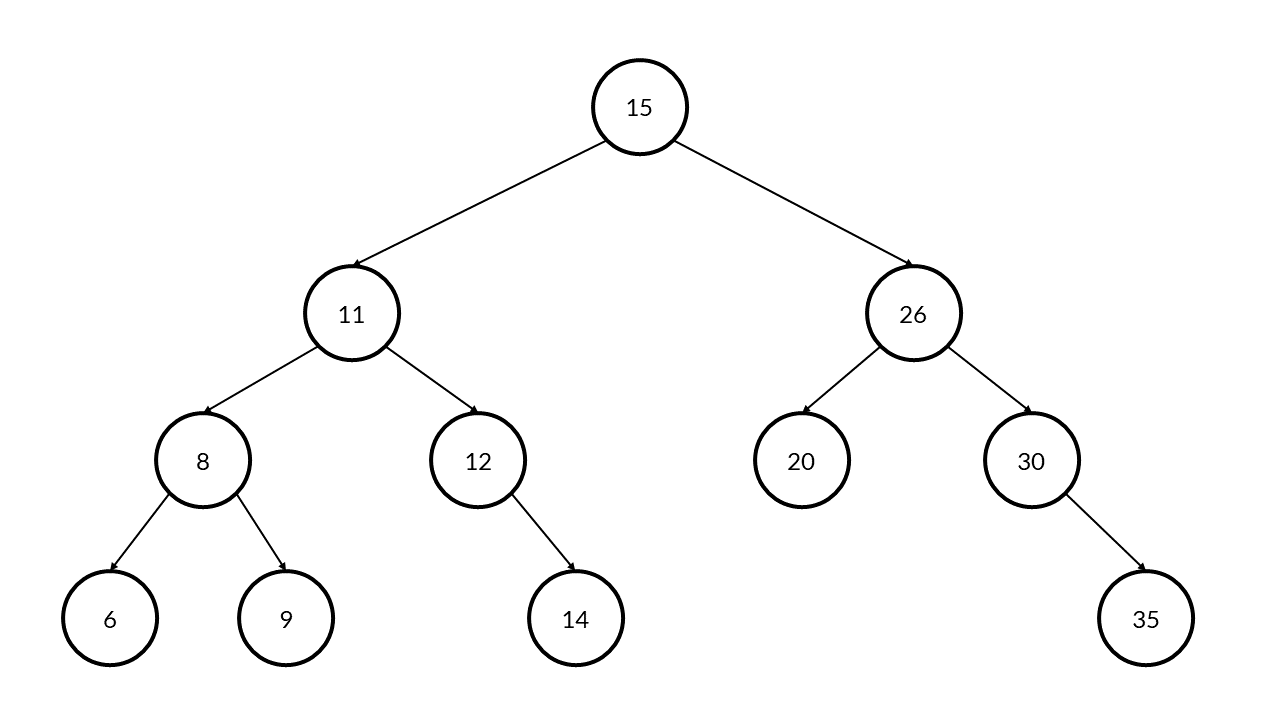
The rules for a binary tree are:

• each node has exactly two edges, a left node and a right node
• nodes to the left are less than the current node
• nodes to the right are greater than the current node

The tree we looked at before is an example of a binary tree. Take a look at each of the nodes and check for yourself that they follow the rules!

Searching Elements

Before we look at the implementation of how to search with code, let’s look at how a binary tree might search for an element. When we are examining the elements within a tree, we always start at the root node, which in a binary tree should be more or less the middle of the data.

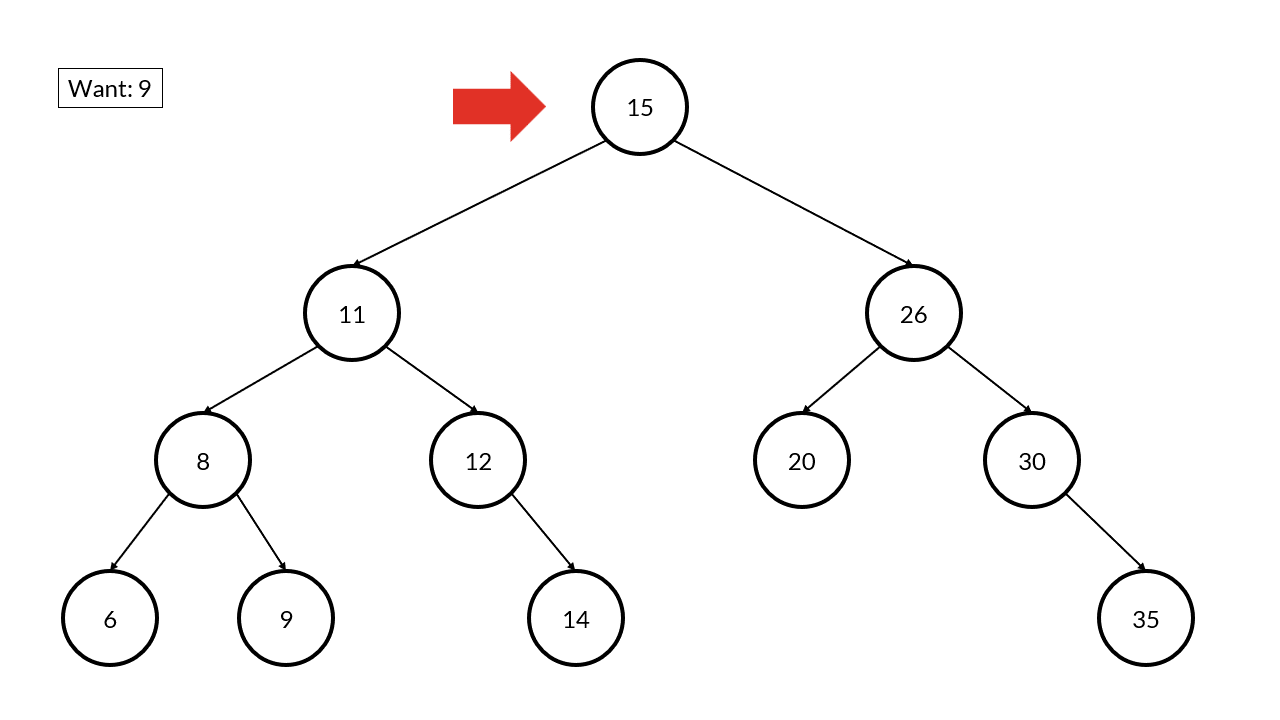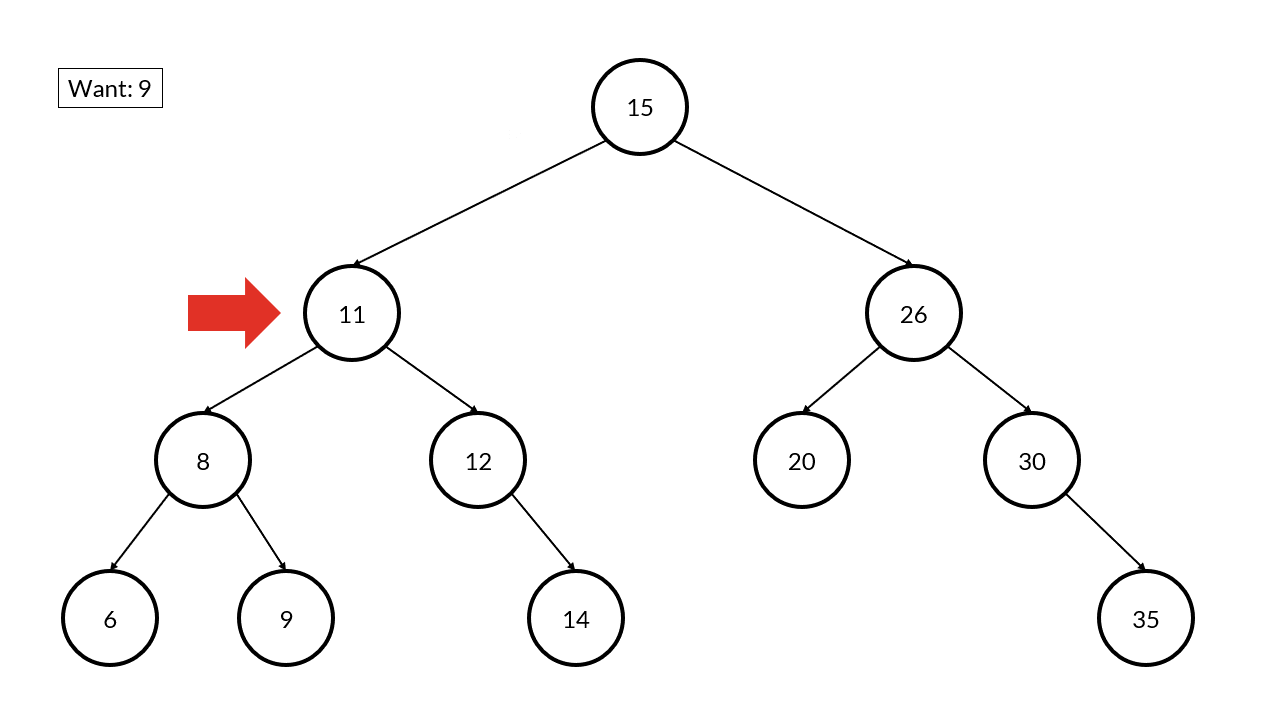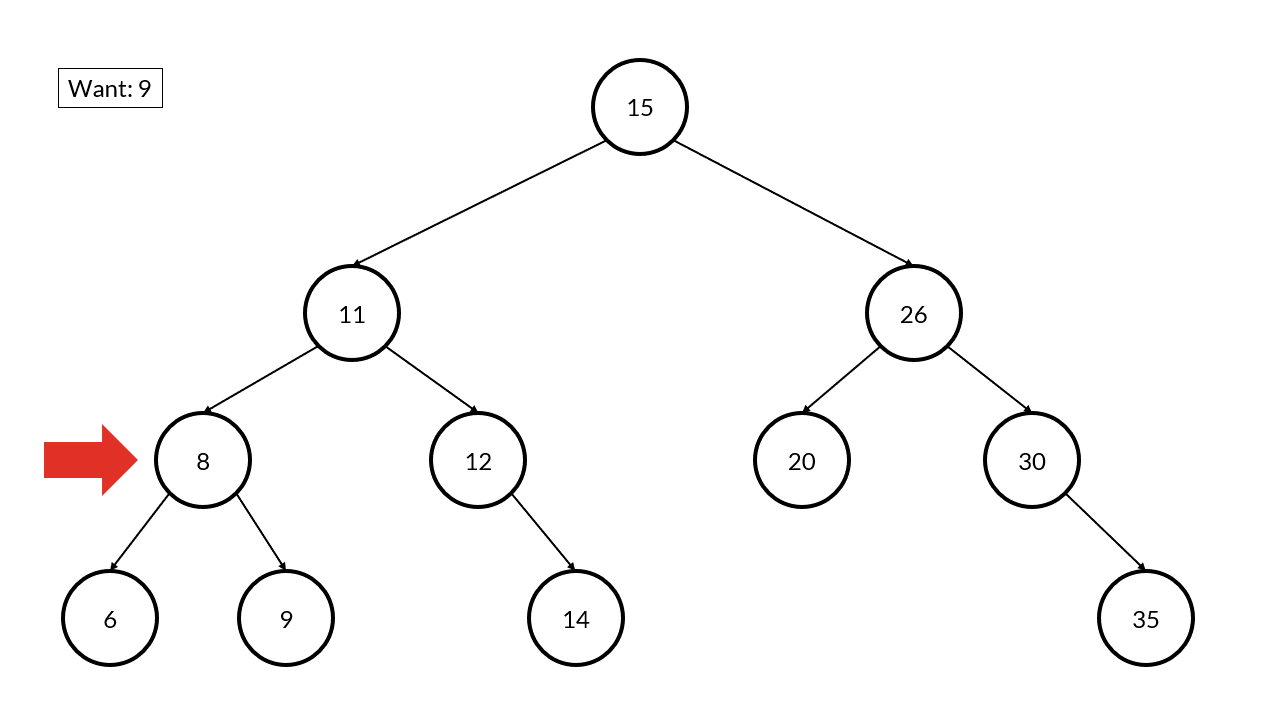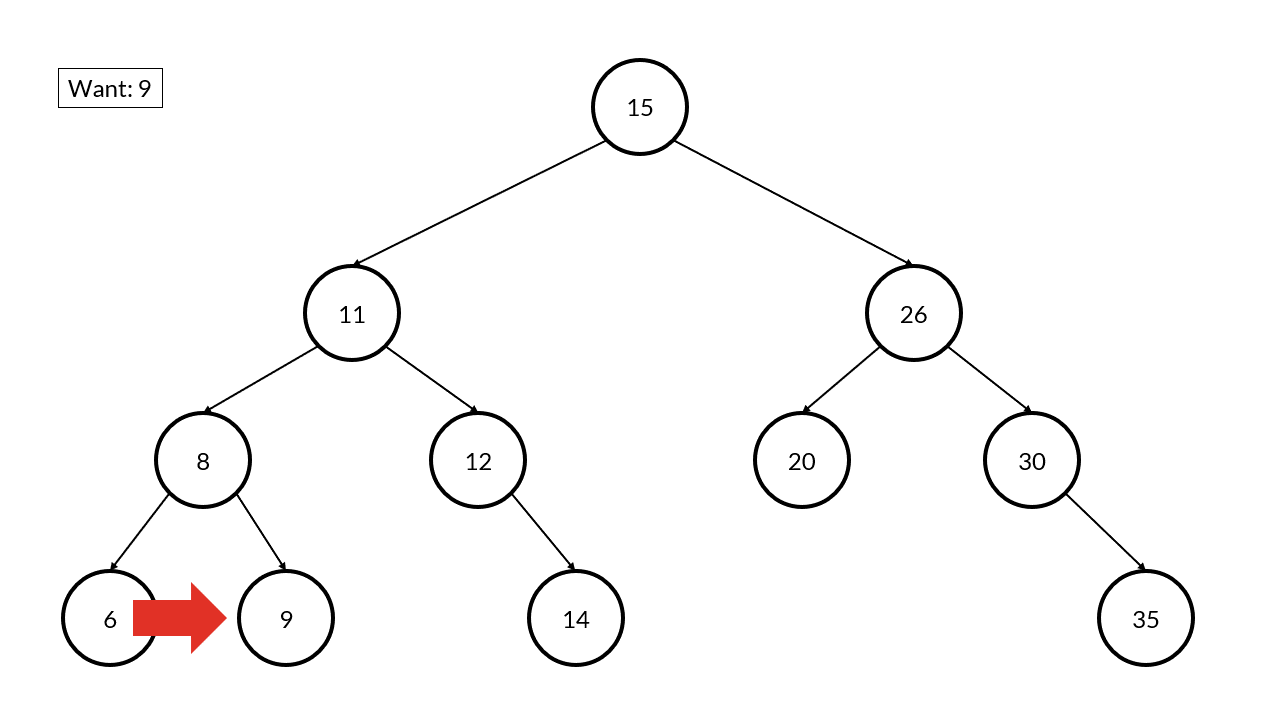
Once we start at the root, we examine the value and ask ourselves “is the value we are looking for less than, equal to, or greater than this value?” If the value is equal, great! We found our answer. If the value we want is less than what we currently have, then we go the left node and ask ourselves the same question. If the value we want is greater than what we currently havbe, then we go to the right node and ask ourselves the same question.

See if you can follow along with this example below. This is the same tree as before and we want to find the value 9.

Traverse Elements

Now that we conceptually understand searching for elements, we can see that searching for elements is just repeating the same operation over and over again. This means that if we program the operation correctly, the entire search algorithm is done.

Imagine we have nodes that are defined like below:

class Node {
    int value;
    Node left;
    Node right;
}

We now can apply the logic for finding the right element that we talked about in the section above. Consider this code snippet:

Node current = root;
if (current.value < desired) {
    current = root.right;
} else if (current.value > desired) {
    current = root.left;
}

We can see that this takes us from one step to the next, we could then use this logic in a for loop until we find the value we want.