Exercise 3 - The Burrows-Wheeler Transform
The Burrows-Wheeler transform (BWT) is an algorithm used in data compression. It takes as an input a string, and outputs an encoded string, which usually has similar characters clustered together.
The Theory
The algorithm is relatively straightforward and easy to understand.
- Take the input string and extract all of its rotational transformations. (See picture).
- Sort the rotations in lexicographical order, ascending.
- Take the last column of the sorted transform; this is the output.
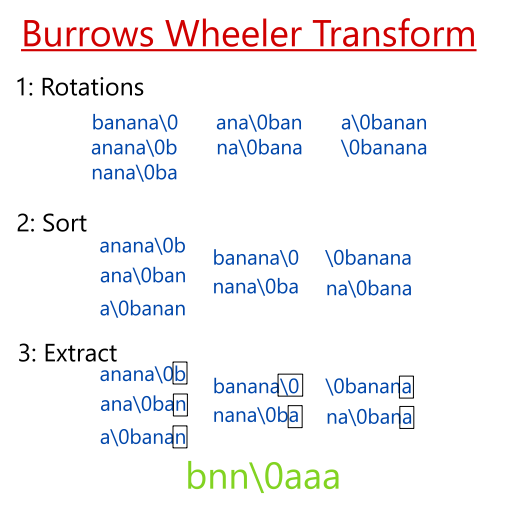
In the diagram above, we use the string banana as an example. The \0 is a symbol used to denote the end of the string (as in the null terminator character in C), but is lexicographically the LARGEST character when compared to the others.
An efficient way to implement the BWT is using a data structure called a suffix array. To create a suffix array, we first take all suffixes of an input string, and give it a numbered label. We then sort the suffixes lexicographically.

Using Nuevo\0 as an example, we first take the suffixes of it and list them out. We then sort them in lexicographic order, with \0 being the null terminating character as before and acting as the largest character. Finally, we take the index of the first letter of each suffix, and put them into an array. For instance, the index of the letter N in Nuevo\0 is 0, while the index of e is 2. Since they are alphabetically the smallest, they go into slots 0 and 1 of the array, respectively.
We can think of suffixes as rotations for the Burrows-Wheeler transform! All we need to do is append the prefix that we “chopped off” to the end of the string. So, evo\0 becomes evo\0Nu when we want to think of the suffix as a rotation. Then, if we do this for all the suffixes, we get the sorted rotations we want in the Burrows-Wheeler transform.
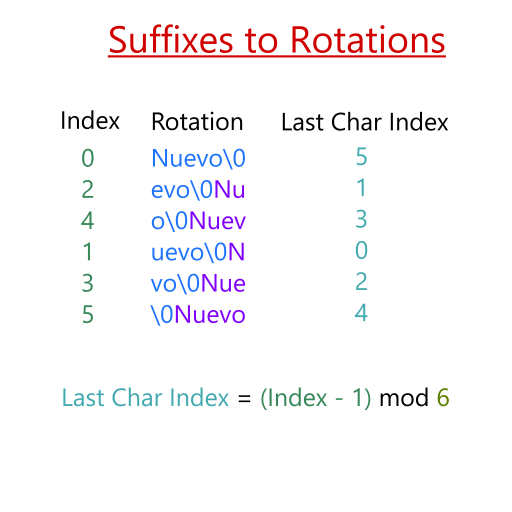
A key note is that we don’t actually need to store the rotations because the index in the suffix array gives us that information already. If suffix_array[i] == 0, then we know that the rotation we’re looking at is Nuevo\0. If suffix_array[i] == 3, then the rotation we’re looking at is vo\0Nue. You can think of it as us rotating N spaces to the right in the case suffix_array[i] == N. The illustration above demonstrates this.
So, with that said, we can get the last character of the rotation simply by taking suffix_array[i] and subtracting by 1, then taking the modulus of the total length of the suffix array to get the index of the original string we are looking for. This gives us the Burrows-Wheeler transform for any given string.
The Implementation
The implementation strategy we use is the one we highlighted above: construct a suffix array, then take the indices, subtract by 1, then perform a modulo operation of the length of the string (including the null terminator).
We’ve implemented the suffix array and with it the Burrows-Wheeler transform. However, we were tired at the time and missed quite a few bugs. This exercise can be tricky because it involves a lot of indexing and figuring out how we can be sneaky with using them. As a hint to fixing the errors, most of the bugs are centered the suffix array and how we use it.
The null terminator character can mess up how you print your strings. In this exercise, you have to print out the transformed string character by character, because the null terminator character will cause the printf function to stop printing after it finds it. The following code will print out the result of calling bwt(dest, src), where STR_LEN is the static length of the string including the null terminator.
for(int i = 0; i < STR_LEN; ++i) {
printf("%c", dest[i]);
}
Note that strlen() returns the length of the string, without the null terminator.
One final tip: % in C is not the modulo operator! It is the remainder operator. Perhaps this is the reason why some indexing has gone wrong…
All functions are documented in bwt.h. Use any tools like gdb and valgrind to your advantage. Good luck!
You did it!
Workshop complete
