Exercise 2 - Binary Heap Implementation

A binary heap is an important data structure used most often to implement a data type called a priority queue. It is also used conceptually in sorting algorithm called heapsort. Its distinctive feature is its O(1) query for the largest or smallest value within its contents, depending on what kind of heap we are talking about.

The Theory

The binary heap is conceptually a complete binary tree. This means that nodes are added to the tree in level order, and the depth of the tree increases only when there is no room the deepest tree level.

In addition to this structural constraint, it follows the heap ordering property: A node’s children must have a value larger or smaller than the node itself. In a min-heap, the children must be larger. In a max-heap, the children must be smaller. Effectively, this means that the root must contain the largest element in the heap.

The following is an example of a max binary heap, which is the type of heap we’ll focus on in this exercise.

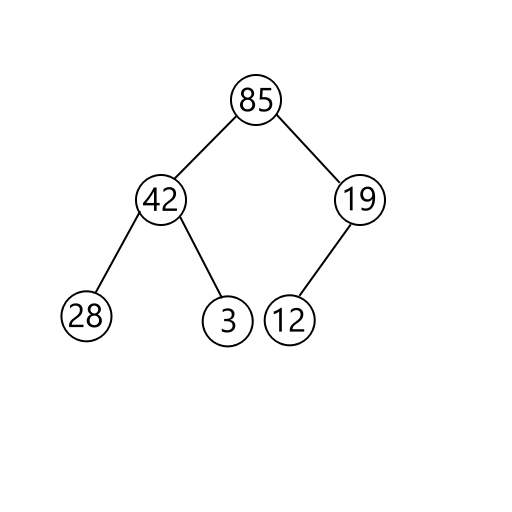
You can see that every node has 2 or no children, except the node on the farthest right. The nodes are filled in from left to right before starting a new row. All children are smaller than their parent.

We can use an array to represent this data structure. A node i can be accessed by its index, i. To access its left child, multiply by 2. To access its right child, multiply by 2 and add 1. The following diagram illustrates this:

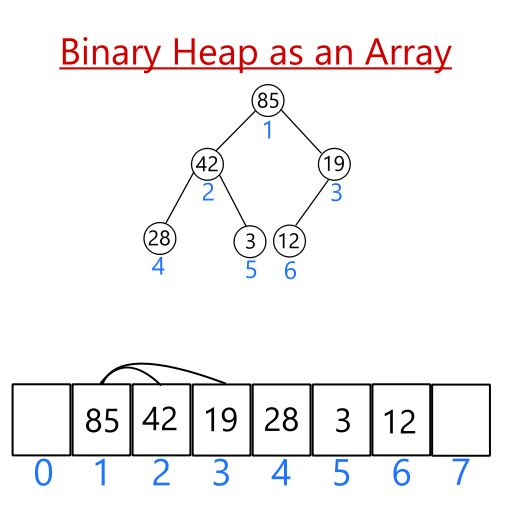
Adding to a binary heap

To add an element, we first add it to the next available spot. Next, we retroactively “fix” any problems caused by this by sliding it up and swapping nodes until it reaches a stable position, i.e. its parent is larger than or equal to itself.

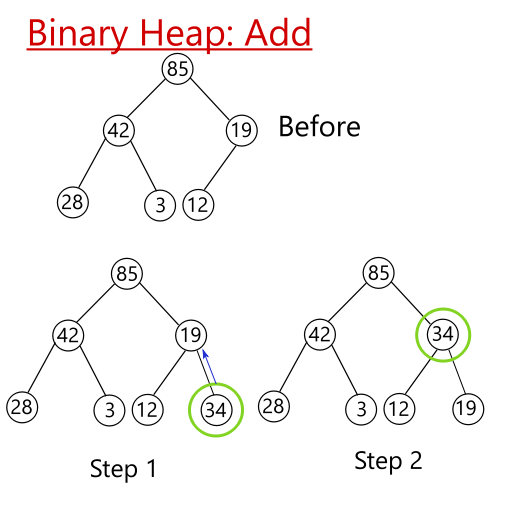
The diagram below illustrates this process for adding 34 to the example binary heap.

1. We insert 34 into the last slot tentatively (green circle, step 1).
2. We then compare with its parent (blue arrow), and find that 34 > 19. Thus, we swap the two nodes.
3. In step 2, we compare with 85, and find that 34 < 85, which indicates that we’re done.

Removing the Max from the Heap

A max binary heap also needs to support removeMax, which removes the largest element in the heap. Luckily, the largest element is simply the root; however, we need to fix the problems caused by this new hole we’ve made.

To fill that hole, we take the last element and fill it in to the top spot. Like before we retroactively “fix” any problems this causes. We repeatedly perform swaps downwards with the smaller child until it reaches a stable position in the heap.

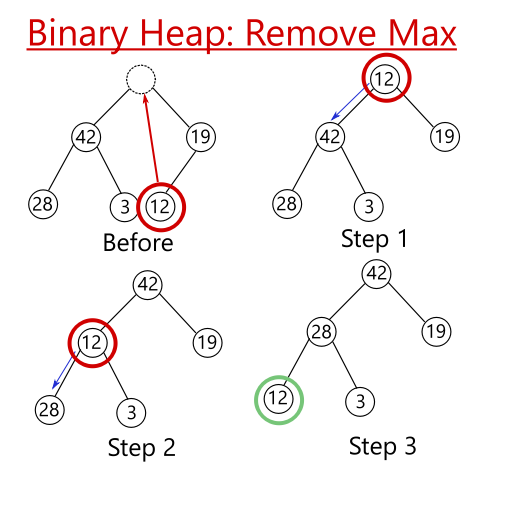
The diagram below shows how a max removal occurs.

1. The root is removed and placed with the element farthest on the right on the bottom row.
2. In step 1, we compare 19 and 42. Since 42 is the larger of the 2, we compare 12 and 42 (blue arrow), and find 12 < 42. Thus, we swap 12 with 42.
3. We repeat the process for step 2. We find 28 is the larger of the 2 children, and since 12 < 28 we swap again.
4. We finally reach a stable position for step 3.

The Implementation

In our implementation, we start indexing from 1 to save a bit of computation. So the root of the binary heap is located in heap.__arr[1] instead of heap.__arr[0]. All the functions have comments about their function in binary_heap.h.

The implementation will be tested against duplicates, so make sure to handle those. Also, while the heap is fixed in size, the data is stored in the heap. Make sure that the data is free’d!

Your goal is to run make test and have no errors. Use any tools, like gdb, valgrind, etc. to your advantage. Good luck!

Launch Replit