Step 1 - Finding the problem (Part 4)

Another Type of Bug: Memory Errors

A C/C++’s nightmare, memory errors are one of the most frustrating kinds of bugs that exist. Failing to address them can result in undefined behavior (non-replicable bugs!) and memory leaks. Thus, fixing them is a huge priority.

Luckily, people have also written programs to help you find memory errors, and one of these programs is valgrind. Valgrind is a tool that not only looks for memory errors, but shows you exactly where the errors occur in your code. Let’s use valgrind to find where memory errors occur. As an example, we have a rudimentary implementation of a vector in C, which is the C++ standard library’s version of a dynamically sized array.

Launch Replit

First make the program using

make Vector

Now run it using

examples/Vector

Notice that there’s an error called a ‘double free’! This is a type of memory caused by calling free to a pointer twice.

Now instead of using gdb, use valgrind to check how memory is allocated and used. Run the command:

valgrind --tool=memcheck --leak-check=full examples/Vector

It should be apparent that valgrind caught some errors, perhaps related to the double free (notice the ERROR SUMMARY at the bottom has a few errors detected!).

Let’s take a look at some of the errors.

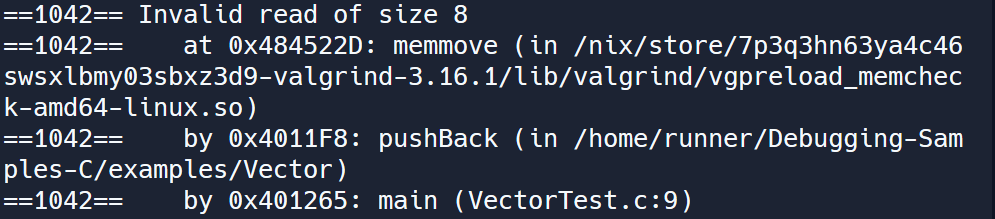
The error shown above is called an invalid read, which is often because you are reading memory that was free’d in another block. Valgrind lets you see where the memory is free’d and alloc’d:

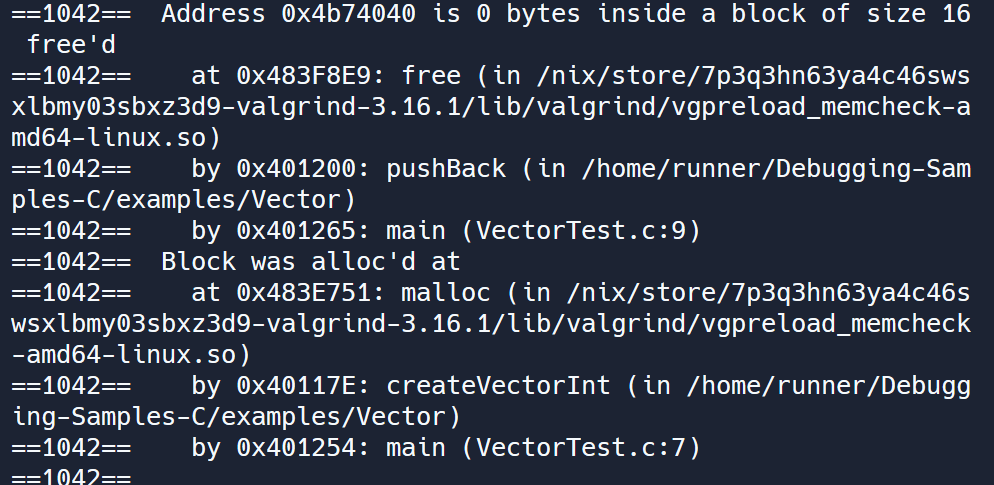
The block of memory was allocated by the malloc function in createVectorInt, which was called in the main function. The block was free’d by the free function called in the pushBack function.

Finally, in the heap summary, you can see that there were 96 bytes that were ’lost’ - in other words, there was a memory leak. This happened because we forgot to call deleteVectorInt on the vector at the end of the main function.

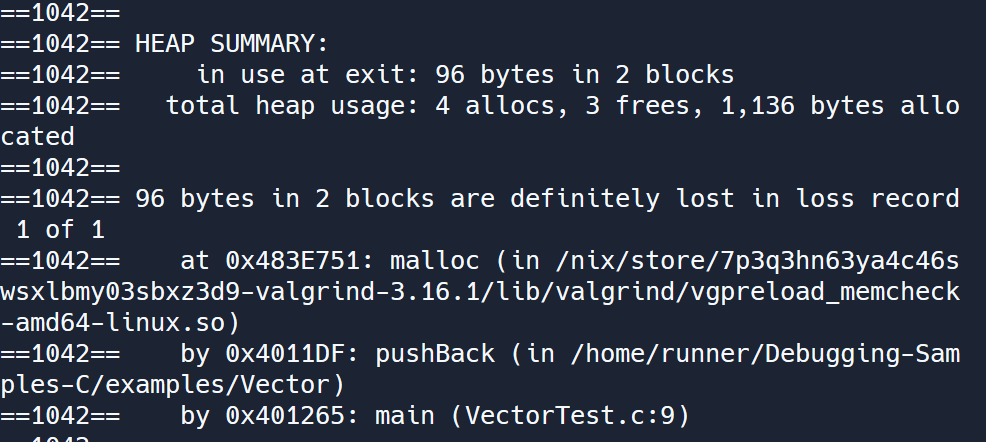
Valgrind provides a plethora of information that you can use to hunt down memory errors in your C and C++ programs. It not only informs you of where errors are happening, but also where memory blocks are allocated and subsequently free’d (or not free’d, in the case of a memory leak). Can you find the bug that causes all the invalid reads in the vector example?

In the exercises, you will be required to fix any memory errors that appear.